振型分解法

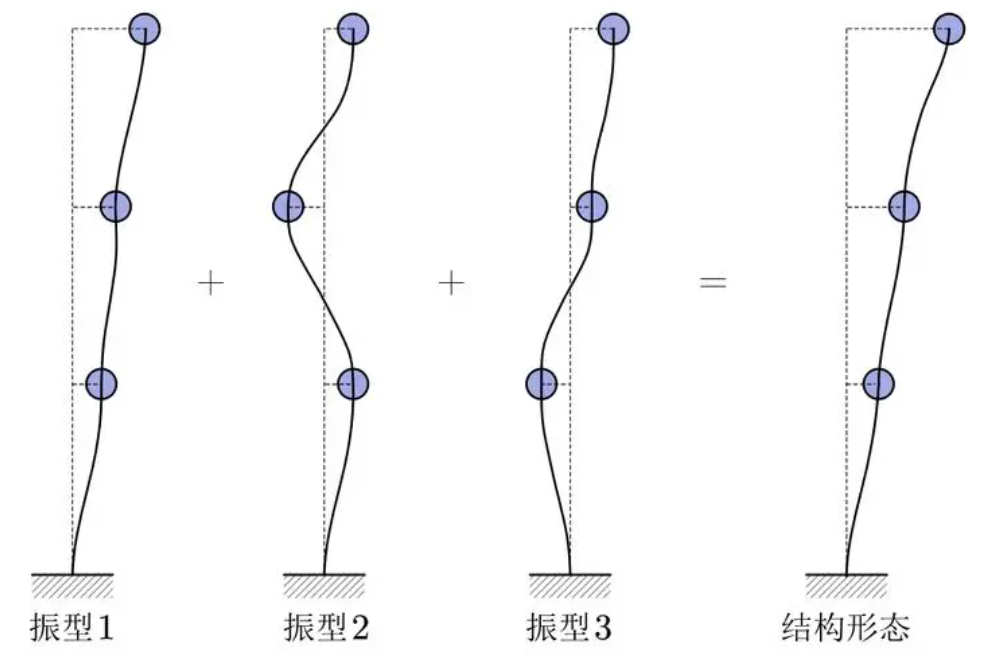
SRSS即 square root of the sum of the squares（振型组合方法）简称“平方和开平方根”。

该方法建立在随机独立事件的概率统计方法之上，也就是说要求参与数据处理的各个事件之间是完全相互独立的，不存在耦合关联关系。

时程分析包括线弹性时程分析和弹塑性时程分析两大类，与振型分解法的主要区别在于采用实测的地震波输入结构计算结构的响应，弹塑性时程分析具体还可分为静力弹塑性时程分析（也称Pushover分析）和动力弹塑性时程分析两类。

主要是由应变率大小来分。在应变率低于10^(-3)/s的，就是静力弹塑性，应变率高于10^(-3)/s的，就是动力弹塑性。应变率是材料相对于时间的应变（变形）的变化，其定义由美国冶金学家Jade LeCocq于1867年首次引入，其定义为“应变发生率，是应变变化的时间率”。 在物理学中，应变速率通常被定义为应变相对于时间的导数。

反应谱分析基于振型分解法反应谱理论，是一种工程上最常用的计算地震作用下结构动力响应方法，但这种方法只限于线弹性结构，弹塑性阶段振型分解法不再适用。

当结构的自振形态或自振频率相差较大时，可近似认为每个振型的振动是相互独立的，因此，采用SRSS方法可以得到很好的结果。当振型的分布在某个区间内比较密集时，也就是说某些振型的频率值比较接近时，这一部分的振型就不适合采用SRSS方法，应当特殊处理之后，再与其他差异较大的振型采用SRSS方法计算。

CQC，即完全二次振型组合，是一种完全组合方法。

CQC( complete quadratic combination，即完全二次振型组合 [1] )振型组合方法是一种完全组合方法，也就是说该方法建立在相关随机事件处理理论之上，该方法考虑了所有事件之间的关联性，在计算公式中引进了一系列互相关系数，但是要想得到这些系数绝非易事。当互相关系数很小的时候，意味着事件之间的关联性很弱，近似可以认为是相互独立的，这时便可以采用SRSS方法来处理。